面试必备：回溯算法详解

前言

我们刷leetcode的时候，经常会遇到回溯算法类型题目。回溯算法是五大基本算法之一，一般大厂也喜欢问。今天跟大家一起来学习回溯算法的套路，文章如果有不正确的地方，欢迎大家指出哈，感谢感谢~

1. 什么是回溯算法？
2. 一道算法题走进回溯算法
3. 回溯算法框架套路
4. leetcode案例分析

1 . 什么是回溯算法

回溯算法，一种通过探索所有可能的候选解来找出所有的解的算法。

它采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现，在反复重复上述的步骤后可能出现两种情况：

• 找到一个可能存在的正确的答案；
• 在尝试了所有可能的分步方法后宣告该问题没有答案。

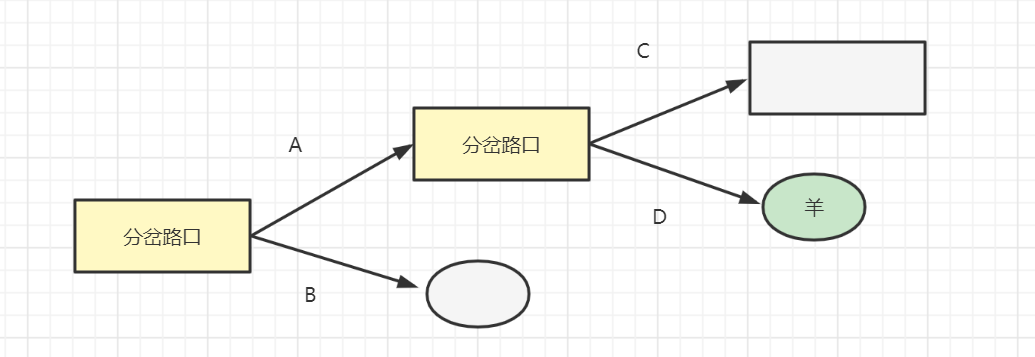
举个类似的生活例子，比如放羊娃的羊在分岔路口走丟了，他顺着不同的岔路口寻找羊，一个岔路口一个岔路口的去尝试找羊。如果找不到羊，继续返回来找到岔路口的另一条路，直到找到羊为止。

如下图为找羊的决策路线图：

放羊娃在A方向找，然后走C方向，没找到时，他回到分岔路，又朝D方向走...直到找到羊，这就是回溯。

2 . 一道算法题走进回溯算法

给定一个不含重复数字的数组 nums ，返回其所有可能的全排列。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

实例2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

2.1 实现思路

看完这道题，我们的第一想法就是穷举全排列呀，但是你不会毫无规律得穷举对吧。比如要排3个数[1,2,3],你会第一位先排1，然后第二位只能是2或者3，如果第二位是2，第三位只能是3了...

我们可以借鉴羊娃找羊的路线图，画出全排列的树图，如下：

其实我们是不是从根节点遍历这棵树，记录下走过路径的数字，走到叶子节点，就可以得到一个排列啦。走完所有的叶子节点，那就可以得到全排列啦。

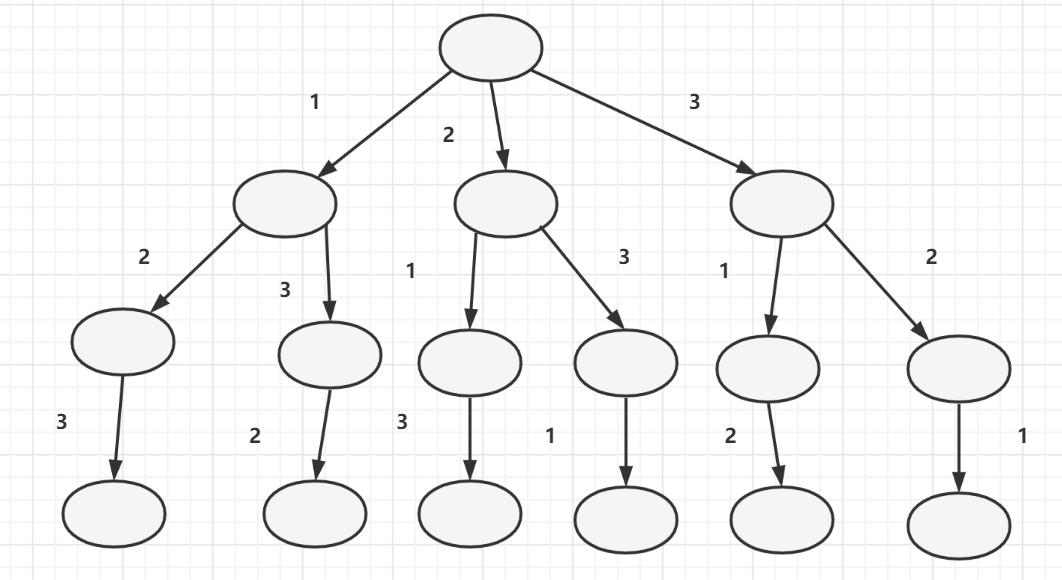
这棵树的如何理解更清晰呢？

• 为了方便理解，我们可以把nums个数k看做k种选择，比如对于[1,2,3]，每一位都有3种选择：1、2、3。
• 每一次做选择，都展开出一棵空间树，
• 选择完后，如果是重复选的路径，就做剪枝。

上图的那颗树，可以看做是遍历所有元素，展开空间树，然后剪枝得来的。如下图

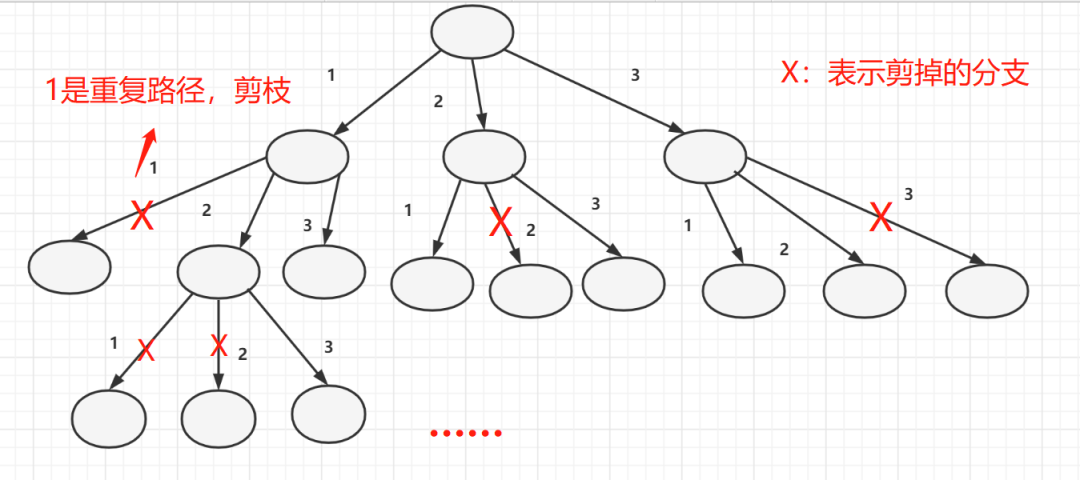
好啦，现在知道树怎么来的，我们来看下怎么遍历找到全排列呢？每次走树的分支，都像是在做决策。我们可以把已走的路径和可做的选择作为树节点的两个属性。

如果在根节点，可做的选择为1、2、3，走过的路径为空，如下图

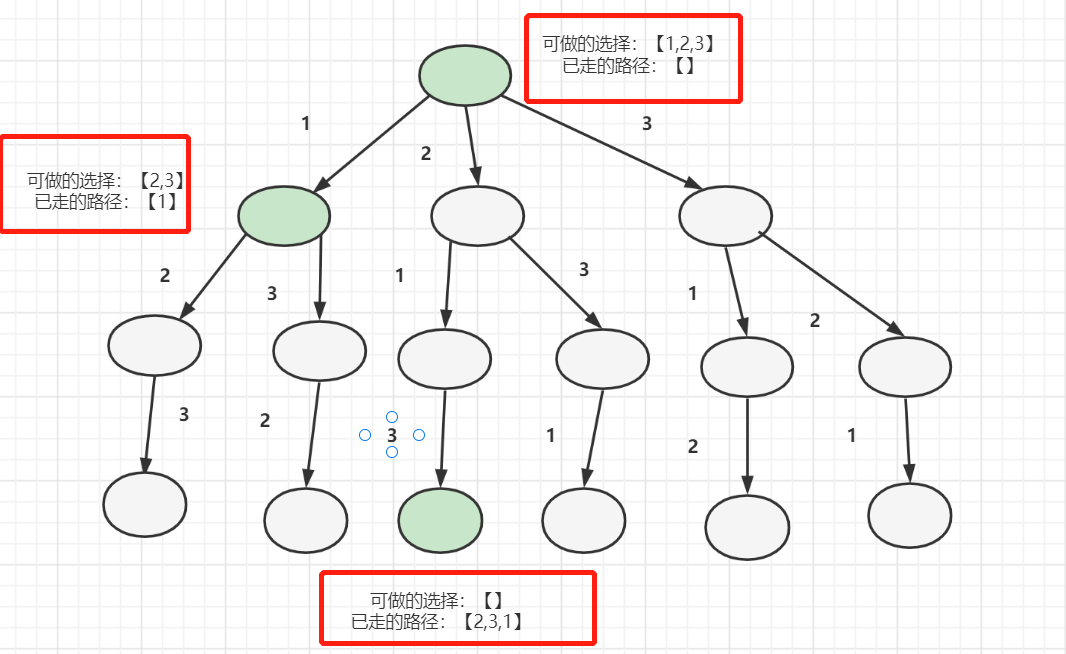
走到叶子节点时，已走路径数组长度等于原素组的个数，这时候走过路径就是满足条件的一个解。

2.2 代码实现

代码怎么写呢？以前我们学习树的遍历，一般都用到递归，这道题也用递归。

• 递归入口是什么呢？一个可选路径和已走过的路径就好啦。
• 递归函数体呢？一个for循环，枚举当前数组的元素，并且需要if判断，以跳过剪枝
• 递归出口呢？也就是走到叶子节点啦，叶子节点，就是当构建的已走路径path的数组长度等于nums的长度

实现代码如下：

class Solution {
    //全排列，即所有路径集合
    List<List<Integer>> allPath = new LinkedList<>();

    public List<List<Integer>> permute(int[] nums) {
        //当前路径，入口路径，path是空的
        List<Integer> path =  new LinkedList<>();
        //递归函数入口，可做选择是nums数组
        backTrace(nums,path);
        return allPath;
    }

    public void backTrace(int[] nums,List<Integer> path){
        //已走路径path的数组长度等于nums的长度,表示走到叶子节点，所以加到全排列集合
        if(nums.length==path.size()){
           allPath.add(new LinkedList(path));
           return;
        }

        for(int i=0;i<nums.length;i++){
            //剪枝，排查已经走过的路径
            if(path.contains(nums[i])){
                continue;
            }
            //做选择，加到当前路径
            path.add(nums[i]);
            //递归，进入下一层的决策
            backTrace(nums,path);
            //取消选择
            path.remove(path.size() - 1);
        }
    }
}

为什么要回溯呢？或者说为什么用到回溯算法呢？

• 因为我们不是要找到一个排列就好了，而是需要找出所有满足条件的排列
• 当递归调用结束时，结束的是当前的递归分支，还需要去别的分支继续找
• 因此需要撤销当前的选择，回到选择前的状态，再选下一个选项，即进入下一个分支。

3 . 回溯算法框架套路

1. 穷举找规律，总结出回溯决策树
2. 套用回溯算法框架代码

3.1. 穷举找规律，总结出回溯决策树

回溯类型问题的问题，基础也是穷举。我们一般通过穷举找到规律，然后画出回溯决策树就好啦。比如以上全排列的例子。

决策树的节点一般有两个属性，就是已走路径和已经可做的选择。在总结决策回溯树的时候需要关注下。

3.2. 套用回溯算法框架

决策一个回溯问题，实际上就是解决一个决策树的遍历过程。需要考虑这三个问题：

• 已走路径：已做出选择，走过的路径
• 可选列表：你当前可以做的选择
• 结束条件：一般走到决策树的叶子节点，它无法再做别的条件选择

回溯算法伪代码框架如下：

//所有路径集合
List<> allPath  = []
void backTrace (可选列表，已走路径)：
     if(满足结束条件){
        allPath.add(已走路径);
        return;
     }
     for(选择：可选列表){
        做选择
        backTrace（当前可选列表，已走路径）;
        撤销选择
     }

4 . leetcode案例分析

题目：

给你一个 无重复元素 的整数数组candidates和一个目标整数target ，找出candidates中可以使数字和为目标数target的所有不同组合 ，并以列表形式返回。你可以按任意顺序 回这些组合。

candidates中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同，则两种组合是不同的。

示例1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

实例2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

4.1 思路

我们先穷举找下规律嘛，拿示例1的数据candidates = [2,3,6,7], target = 7：

7 = 2 + 2 + 3
7 = 7

再拿示例2的数据：

8 = 2+ 2 + 2 +2
8 = 2 + 3 + 3
8 = 3 + 5

其实规律还是比较清晰的，我们只需要把target一个一个减去candidates数组的元素，如果可以减到为0，那么就是一个解。

接下来我们就是画树啦，可以把target当做树的根节点，然后分支分别表示减去candidates数组的中元素，然后子节点就是target减去数组元素的差，如下：

接下来我们可以套用回溯算法框架啦，已走路径，可选列表，结束条件分别怎么表示呢？看下下图：

如果走到橙色节点4这个位置，可选列表就是减2，或者减3啦，因为减6的话为负数啦。怎么确定是可选列表呢？只要当前的target减去要选分支的值大于0，都可以作为可选列表。

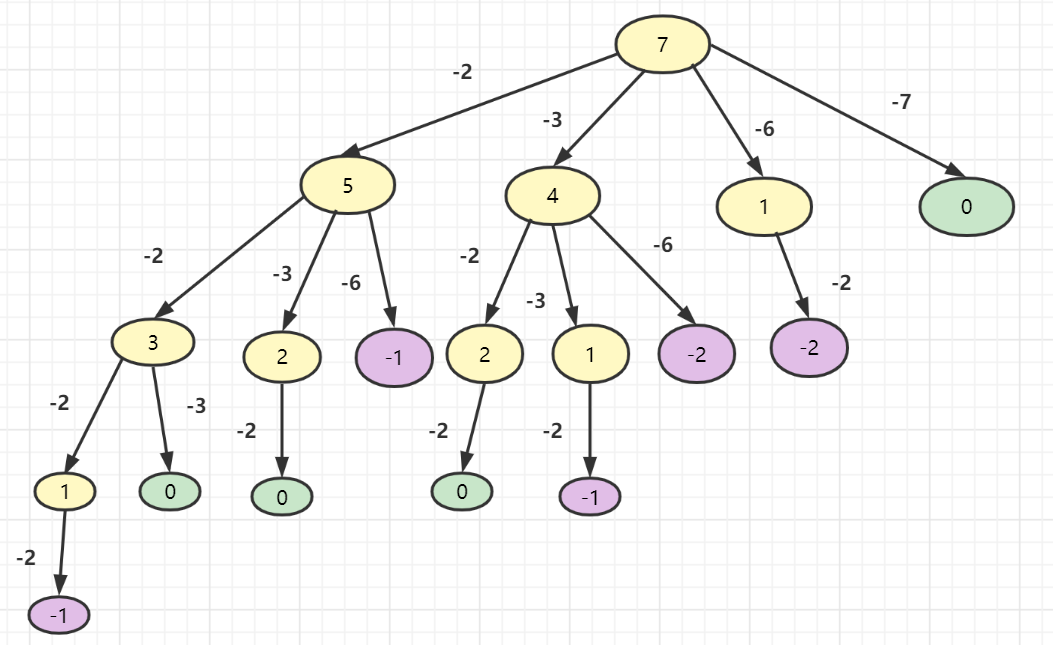
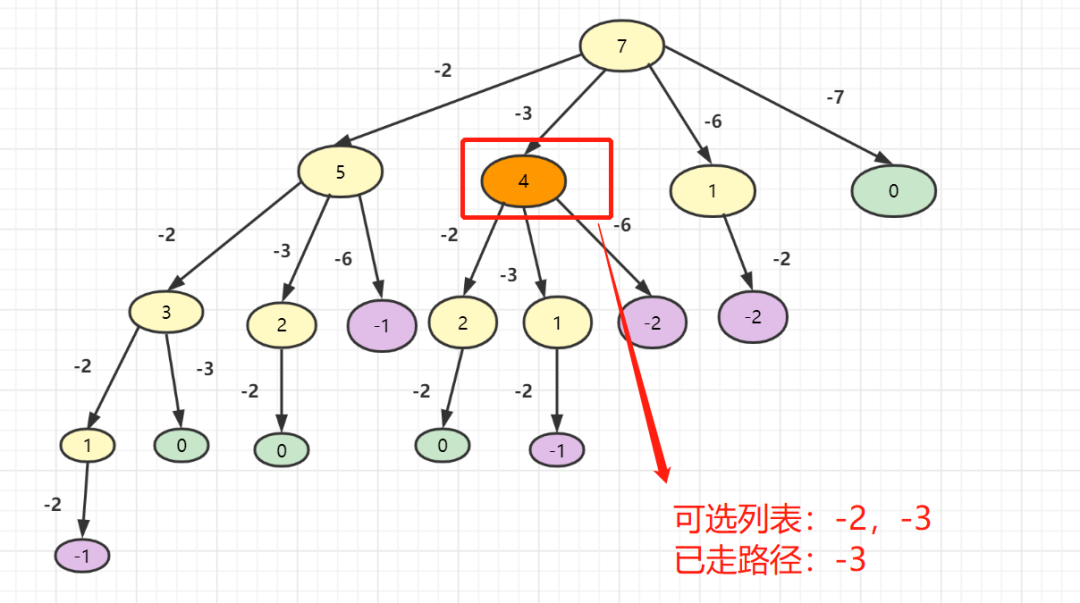
已走路径就是 -3这个分支。

结束条件呢？当走到负数或者0的节点，都表示该结束啦，已经无法决策啦。

4.2 代码实现

最后我们套下溯算法框架伪代码,如下：

class Solution {

    List<List<Integer>> allPath = new LinkedList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<Integer> path = new LinkedList<>();
        backTrace(candidates,target,path,0);
        return allPath;
    }

    public void backTrace(int[] candidates,int target, List<Integer> path,int start){

        if (target < 0) {
            return ;
        }
        //满足结束条件，加到总路径
        if(target==0){
            allPath.add(new ArrayList(path));
            return;
        }

        for (int i = start; i < candidates.length; i++) {
            //可选列表：当前结点大于要走的路径数值
            if (target >= candidates[i]) {
                //做选择
                path.add(candidates[i]);
                //递归
                backTrace(candidates, target - candidates[i], path, i);
                //撤销选择
                path.remove(path.size() - 1);
            }

        }
    }
}

参考与感谢

• 《labuladong的算法小抄》
• leetcode官网

本文由哈喽比特于2年以前收录，如有侵权请联系我们。
文章来源：https://mp.weixin.qq.com/s/fz9bQPGmInnaj9vvzdizJw