第3章基础表达式

为了简化代码，我们从基础表达式开始。基础表达式是指完全由数值型面值和标识符组成的表达式。

3.1 基础表达式语法

基础表达式主要是指由一元和二元运算符组成的表达式，运算的主体是各种面值或标识符。基础表达式语法如下：

Expression = UnaryExpr | Expression binary_op Expression .
UnaryExpr  = Operand | unary_op UnaryExpr .
Operand    = Literal | identifier | "(" Expression ")" .

binary_op  = "||" | "&&" | rel_op | add_op | mul_op .
rel_op     = "==" | "!=" | "<" | "<=" | ">" | ">=" .
add_op     = "+" | "-" | "|" | "^" .
mul_op     = "*" | "/" | "%" | "<<" | ">>" | "&" | "&^" .

unary_op   = "+" | "-" | "!" | "^" | "*" | "&" | "<-" .

其中Expression表示基础表达式的递归定义，可以是UnaryExpr类型的一元表达式，或者是binary_op生成的二元表达式。而基础表达式运算符两边的对象由Operand定义，主要是面值或表达式，也可以是由小括弧包含的表达式。

3.2 解析表达式

parser.ParseExpr函数是解析的单个表达式（可以包含注释），因此返回的ast.Expr是一个表达式抽象接口：

type Expr interface {
    Node
    // contains filtered or unexported methods
}

除了内置一个ast.Node接口之外没有任何其它信息和约束（这是Go语言隐式接口的缺点，用户需要自己猜测接口之间的逻辑关系）。

而ast.Node接口更简单，只有两个方法表示了这个语法树结点的开始位置和结束位置：

type Node interface {
    Pos() token.Pos // position of first character belonging to the node
    End() token.Pos // position of first character immediately after the node
}

通过分析go/ast包的文档可以发现很多类型以Expr为后缀名：

$ go doc go/ast | grep Expr
type BadExpr struct{ ... }
type BinaryExpr struct{ ... }
type CallExpr struct{ ... }
type Expr interface{ ... }
type ExprStmt struct{ ... }
type IndexExpr struct{ ... }
type KeyValueExpr struct{ ... }
type ParenExpr struct{ ... }
type SelectorExpr struct{ ... }
type SliceExpr struct{ ... }
type StarExpr struct{ ... }
type TypeAssertExpr struct{ ... }
type UnaryExpr struct{ ... }

真实的表达式种类当然并不仅仅是这些，起码前面例子中的ast.BasicLit类型不在其中，不过目前我们并不需要Expr的全部类型列表。

我们以ast.BinaryExpr表达的二元算术表达式开始，因为加减乘除四则运算是我们最熟悉的表达式结构：

func main() {
    expr, _ := parser.ParseExpr(`1+2*3`)
    ast.Print(nil, expr)
}

输出的结果如下：

 0  *ast.BinaryExpr {
 1  .  X: *ast.BasicLit {
 2  .  .  ValuePos: 1
 3  .  .  Kind: INT
 4  .  .  Value: "1"
 5  .  }
 6  .  OpPos: 2
 7  .  Op: +
 8  .  Y: *ast.BinaryExpr {
 9  .  .  X: *ast.BasicLit {
10  .  .  .  ValuePos: 3
11  .  .  .  Kind: INT
12  .  .  .  Value: "2"
13  .  .  }
14  .  .  OpPos: 4
15  .  .  Op: *
16  .  .  Y: *ast.BasicLit {
17  .  .  .  ValuePos: 5
18  .  .  .  Kind: INT
19  .  .  .  Value: "3"
20  .  .  }
21  .  }
22  }

下图是parser.ParseExpr("1+2*3")返回的树结构：

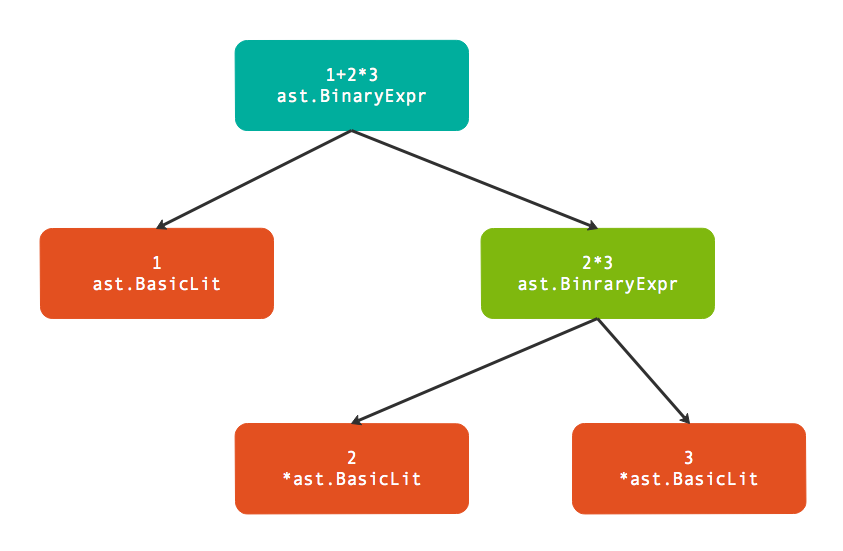
其中ast.BasicLit是基础面值类型，在前面章节已经讲过。而ast.BinaryExpr是表示二元表达式的结点，其定义如下：

type BinaryExpr struct {
    X     Expr        // left operand
    OpPos token.Pos   // position of Op
    Op    token.Token // operator
    Y     Expr        // right operand
}

其中Op成员表示二元运算符，而X和Y成员则对应运算符左右两个操作数。最重要的是，X和Y操作数都是Expr接口类型，这就可以构成递归定义！因此在输出的结果中，最外层的Y部分被填充为*ast.BinaryExpr类型的子语法树（这说明后出现的乘法有着更高的优先级）。

3.3 求值表达式

在了解了ast.BinaryExpr语法树的结构之后，其实我们就可以手工对表达式求值了：

func main() {
    expr, _ := parser.ParseExpr(`1+2*3`)
    fmt.Println(Eval(expr))
}

func Eval(exp ast.Expr) float64 {
    switch exp := exp.(type) {
    case *ast.BinaryExpr:
        return EvalBinaryExpr(exp)
    case *ast.BasicLit:
        f, _ := strconv.ParseFloat(exp.Value, 64)
        return f
    }
    return 0
}

func EvalBinaryExpr(exp *ast.BinaryExpr) float64 {
    switch exp.Op {
    case token.ADD:
        return Eval(exp.X) + Eval(exp.Y)
    case token.MUL:
        return Eval(exp.X) * Eval(exp.Y)
    }
    return 0
}

其中Eval函数用于递归解析表达式，如果是二元表达式*ast.BinaryExpr类型则调用EvalBinaryExpr进行解析，如果是*ast.BasicLit面值类型则直接用strconv.ParseFloat解析浮点数面值。EvalBinaryExpr函数用于解析二元表达式，这里为了简单只展示的加法和乘法类型的运算符，然后在加法或乘法的左右子表达式中再调用Eval解析。

Go语言中，表达式是所有运算的基础。很多功能性的函数也可以作为表达式的一个部分参与运算。如果表达式中再引入变量和函数就变得异常强大了。

3.4 标识符：为表达式中引入变量

在前面的例子中，我们已经尝试过数值类型的常量构成的表达式求值。我们现在尝试为表达式引入变量，变量由外部动态注入。

还是先从一个简单的例子入手：

func main() {
    expr, _ := parser.ParseExpr(`x`)
    ast.Print(nil, expr)
}

输出结果如下：

0  *ast.Ident {
1  .  NamePos: 1
2  .  Name: "x"
3  .  Obj: *ast.Object {
4  .  .  Kind: bad
5  .  .  Name: ""
6  .  }
7  }

表达式只有一个x，对应*ast.Ident类型。*ast.Ident类型的定义如下：

type Ident struct {
    NamePos token.Pos // identifier position
    Name    string    // identifier name
    Obj     *Object   // denoted object; or nil
}

其中最重要的是Name成员，表示标识符的名字。这样我们就可以在递归解析时传入一个上下文参数，其中包含变量的值：

func main() {
    expr, _ := parser.ParseExpr(`1+2*3+x`)
    fmt.Println(Eval(expr, map[string]float64{
        "x": 100,
    }))
}

func Eval(exp ast.Expr, vars map[string]float64) float64 {
    switch exp := exp.(type) {
    case *ast.BinaryExpr:
        return EvalBinaryExpr(exp, vars)
    case *ast.BasicLit:
        f, _ := strconv.ParseFloat(exp.Value, 64)
        return f
    case *ast.Ident:
        return vars[exp.Name]
    }
    return 0
}

func EvalBinaryExpr(exp *ast.BinaryExpr, vars map[string]float64) float64 {
    switch exp.Op {
    case token.ADD:
        return Eval(exp.X, vars) + Eval(exp.Y, vars)
    case token.MUL:
        return Eval(exp.X, vars) * Eval(exp.Y, vars)
    }
    return 0
}

在Eval函数递归解析时，如果当前解析的表达式语法树结点是*ast.Ident类型，则直接从vars表格查询结果。

不过在Go语言的表达式要复杂很多，不仅仅有普通的局部变量，还有数组索引求值、管道取值、其它结构的成员求值等类型。但是标识符是引入变量最基础的方法，我们可以在此基础方法之上慢慢完善更复杂的求值函数。

Go语法树入门

第3章 基础表达式

3.1 基础表达式语法

3.2 解析表达式

3.3 求值表达式

3.4 标识符：为表达式中引入变量

第3章基础表达式