3.4 节的练习

3.4.1

给出识别练习 3.3.2 中各个正则表达式所描述的语言状态转换图。

解答

解答步骤：NFA -> DFA -> 最少状态的 DFA（状态转换图）

1. a(a|b)*a

   NFA:

   

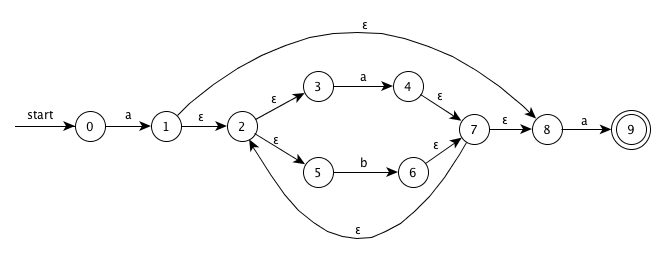
   DFA:

   NFA	DFA	a	b
   {0}	A	B
   {1,2,3,5,8}	B	C	D
   {2,3,4,5,7,8,9}	C	C	D
   {2,3,5,6,7,8}	D	C	D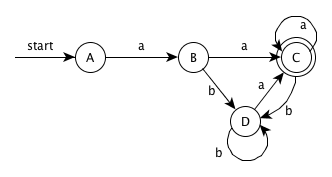

   

   最少状态的 DFA(状态转换图):

   合并不可区分的状态 B 和 D

   

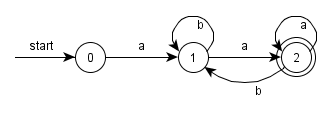
2. ((ε|a)b*)*

   

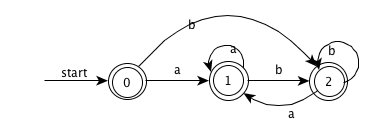
3. (a|b)*a(a|b)(a|b)

   NFA:

   

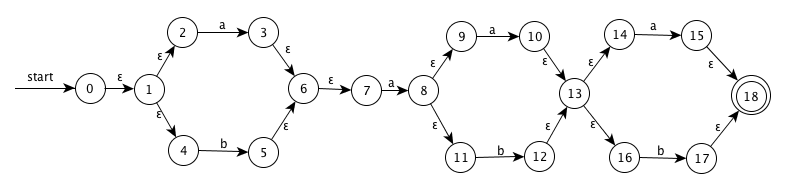
   DFA:

   NFA	DFA	a	b
   {0,1,2,4,7}	A	B	C
   {1,2,3,4,6,7,8,9,11}	B	D	E
   {1,2,4,5,6,7}	C	B	C
   {1,2,3,4,6,7,8,9,10,11,13,14,16}	D	F	G
   {1,2,4,5,6,7,12,13,14,16}	E	H	I
   {1,2,3,4,6,7,8,9,10,11,13,14,15,16,18}	F	F	G
   {1,2,4,5,6,7,12,13,14,16,17,18}	G	H	I
   {1,2,3,4,6,7,8,9,11,15,18}	H	D	E
   {1,2,4,5,6,7,17,18}	I	B	C

   最少状态的 DFA(状态转换图):

   合并不可区分的状态 A 和 C

   

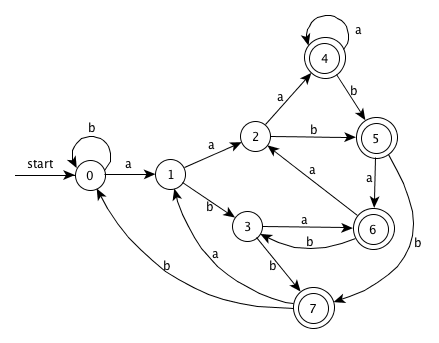
4. a*ba*ba*ba*

   

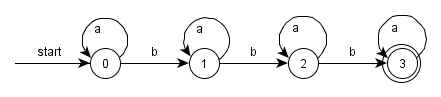
3.4.2

给出识别练习 3.3.5 中各个正则表达式所描述语言的状态转换图。

3.4.3

构造下列串的失效函数。

1. abababaab
2. aaaaaa
3. abbaabb

解答

代码详见：src/failure-function.js

1. [ 0, 0, 1, 2, 3, 4, 5, 1, 2 ]
2. [ 0, 1, 2, 3, 4, 5 ]
3. [ 0, 0, 0, 1, 1, 2, 3 ]

3.4.4 ！

对 s 进行归纳，证明图 3-19 的算法正确地计算出了失效函数。

图 3-19：计算关键字 b_1b_2…b_n 的失效函数

01  t = 0;
02  f(1) = 0;
03  for (s = 1; s < n; s ++){
04      while( t > 0 && b_s+1 != b_t+1) t = f(t);
05      if(b_s+1 == b_t+1){
06          t = t + 1;
07          f(s + 1) = t;
08      }else{
09          f(s + 1) = 0;
10      }
11  }

证明

1. 已知 f(1) = 0

2. 在第 1 次 for 循环时，计算 f(2) 的值，当第5行代码 b_2 == b_1 成立时，代码进入到第7行得出 f(2) = 1，不成立时，则代码进入第9行得出 f(2) = 0。显然，这次循环正确的计算出了 f(2) 。

3. 假设在第 i-1 次进入循环时，也正确的计算出了 f(i)，也有 f(i) = t (无论 t 是大于 0 还是等于 0)

4. 那么在第 1 次进入循环时，分两种情况进行考虑：

   1. t == 0

      这种情况比较简单，直接从第 5 行开始，当 b_i+1 == b_1 时，f(i+1) = 1，否则 f(i+1) = 0

   2. t > 0 while 循环会不断缩小 t 值，试图找出最大可能的使得 b_i+1 == b_t+1 成立的 t 值，如果找到了，则进入第 5 行执行，得到 f(i+1) = t+1；或者直到 t == 0 时也没有找到，则跳出循环，这时进入第 5 行执行，过程类似于前一种情况。

3.4.5 ！！

说明图 3-19 中的第 4 行的复制语句 t = f(t) 最多被执行 n 次。进而说明整个算法的时间复杂度是 O(n)，其中 n 是关键字长度。

解答

详见 matrix 的博文 KMP算法详解。

3.4.6

应用 KMP 算法判断关键字 ababaa 是否为下面字符串的子串：

1. abababaab
2. abababbaa

解答

代码详见：src/failure-function.js

1. true
2. false

3.4.7 ！！

说明图 3-20 中的算法可以正确的表示输入关键字是否为一个给定字符串的子串。

图 3-20：KMP 算法在 O(m + n) 的时间内检测字符串a_1a_3...a_n 中是否包含单个关键字 b1b2...bn

s = 0;
for(i = 1; i <= m; i ++){
    while(s > 0 && a_i != b_s+1) s = f(s);
    if(a_i == b_s+1) s = s + 1;
    if(s == n) return "yes";
}
return "no";

3.4.8

假设已经计算得到函数 f 且他的值存储在一个以 s 为下标的数字中，说明图 3-20 中算法的时间复杂度为 O(m + n)。

解答

详见 matrix 的博文 KMP算法详解。

3.4.9

Fibonacci 字符串的定义如下：

1. s1 = b
2. s2 = a
3. 当 k > 2 时， s_k = s_k-1 s_k-2

例如：s₃ = ab, s₄ = aba, s₅ = abaab

1. s_n 的长度是多少？
2. 构造 s₆ 的失效函数。
3. 构造 s₇ 的失效函数。
4. ！！ 说明任何 s_n 的失效函数都可以被表示为：f(1) = f(2) = 0，且对于 2 < j <= |s_n|, f(j) = j - |s_k-1|，其中 k 是使得 |s_k| <= j + 1 的最大整数。
5. ！！ 在 KMP 算法中，当我们试图确定关键字 s_k 是否出现在字符串 s_k+1 中，最多会连续多少次调用失效函数？

解答

1. 见 维基百科

2. s₆ = abaababa

   failure = [ 0, 0, 1, 1, 2, 3, 2, 3 ]

3. s₇ = abaababaabaab

   failure = [ 0, 0, 1, 1, 2, 3, 2, 3, 4, 5, 6, 4, 5 ]