编译原理(紫龙书)中文第2版习题答案
- 前言
- Exercises for Section 1.1
- Exercises for Section 1.3
- Exercises for Section 1.6
- Exercises for Section 2.2
- Exercises for Section 2.3
- Exercises for Section 2.4
- Exercises for Section 2.6
- Exercises for Section 2.8
- 第2章要点
- Exercises for Section 3.1
- Exercises for Section 3.3
- Exercises for Section 3.4
- Exercises for Section 3.5
- Exercises for Section 3.6
- Exercises for Section 3.7
- Exercises for Section 3.8
- Exercises for Section 3.9
- 第3章要点
- Exercises for Section 4.2
- Exercises for Section 4.3
- Exercises for Section 4.4
- Exercises for Section 4.5
- Exercises for Section 4.6
- Exercises for Section 4.7
- 第4章要点
- Exercises for Section 5.1
- Exercises for Section 5.2
- Exercises for Section 5.3
- Exercises for Section 5.4
- Exercises for Section 5.5
- Exercises for Section 6.1
- Exercises for Section 6.2
- Exercises for Section 6.3
- Exercises for Section 6.4
- Exercises for Section 6.5
- Exercises for Section 6.6
- Exercises for Section 6.7
- Exercises for Section 7.2
- Exercises for Section 7.3
- Exercises for Section 7.4
- Exercises for Section 7.5
- Exercises for Section 7.6
- Exercises for Section 7.7
- Exercises for Section 8.2
- Exercises for Section 8.3
- Exercises for Section 8.4
- Exercises for Section 8.5
- Exercises for Section 12.3
Exercises for Section 3.9
3.9.1
Extend the table of Fig. 3.58 to include the operators
- ?
-
Answer
| node n | nullable(n) | firstpos(n) |
|---|---|---|
| n = c_1 ? | true | firstpos(c_1) |
| n = c_1 + | nullable(c_1) | firstpos(c_1) |
3.9.2
Use Algorithm 3.36 to convert the regular expressions of Exercise 3.7.3 directly to deterministic finite automata.
Answer
-
(a|b)*
-
Syntax tree
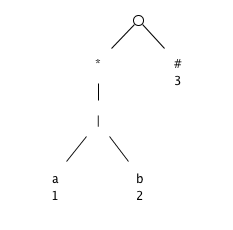
-
firstpos and lastpos for nodes in the syntax tree
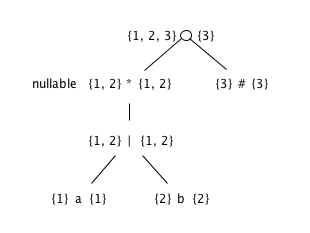
-
The function followpos
node n followpos(n) 1 {1, 2, 3} 2 {1, 2, 3} 3 ∅ -
Steps
The value of firstpos for the root of the tree is {1, 2, 3}, so this set is the start state of D. Call this set of states A. We compute Dtran[A, a] and Dtran[A, b]. Among the positions of A, 1 correspond to a, while 2 correspond to b. Thus Dtran[A, a] = followpos(1) = {1, 2, 3}, Dtran[A, b] = followpos(2) = {1, 2, 3}. Both the results are set A, so dose not have new state, end the computation.
-
DFA
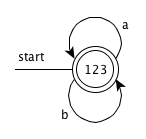
-
-
(a*|b*)*
-
((ε|a)|b*)*
-
(a|b)*abb(a|b)*
3.9.3 !
We can prove that two regular expressions are equivalent by showing that their minimum-state DFA's are the same up to renaming of states. Show in this way that the following regular expressions: (a|b)*, (a*|b*)*, and ((ε|a)b*)* are all equivalent. Note: You may have constructed the DFA's for these expressions in response to Exercise 3.7.3.
Answer
Refer to the answers of 3.7.3 and 3.9.2-1
3.9.4 !
Construct the minimum-state DFA's for the following regular expressions:
- (a|b)*a(a|b)
- (a|b)*a(a|b)(a|b)
- (a|b)*a(a|b)(a|b)(a|b)
Do you see a pattern?
3.9.5 !!
To make formal the informal claim of Example 3.25, show that any deterministic finite automaton for the regular expression
(a|b)*a(a|b)...(a|b)
where (a|b) appears n - 1 times at the end, must have at least 2n states. Hint: Observe the pattern in Exercise 3.9.4. What condition regarding the history of inputs does each state represent?